
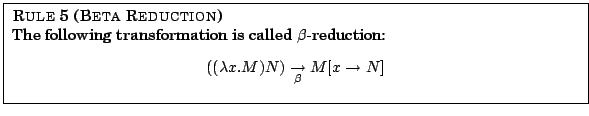
The problem you came up with can be solved with only Alpha Conversion, and Beta Reduction, Don't be daunted by how long the process below is. This means we substitute occurrences of param in output, and that is what it reduces down to I'm going to use the following notation for substituting the provided input into the output: You said to focus on beta reduction, and so I am not going to discuss eta conversion in the detail it deserves, but plenty of people gave their go at it on the cs theory stack exchange On the Notation for Beta Reduction: Consider (λx.(λy.yy)x), this is equivalent through eta reduction to (λy.yy), because f = (λy.yy), which does not have an x in it, you could show this by reducing it, as it would solve to (λx.xx), which is observably the same thing. if It actually makes complete sense but is better shown through an example. All that really means is λx.(f x) = f if f does not make use of x.
Lambda calculus beta reduction examples free#
You may see it written on wikipedia or in a textbook as "Eta-conversion converts between λx.(f x) and f whenever x does not appear free in f", which sounds really confusing.

Find all occurrences of the parameter in the output, and replace them with the input and that is what it reduces to, so (λx.xy)z => xy with z substituted for x, which is zy.Ģ.5) Eta Conversion/Eta Reduction - This is special case reduction, which I only call half a process, because it's kinda Beta Reduction, kinda, as in technichally it's not. z is the input, x is the parameter name, xy is the output. Take (λx.xy)z, the second half of (λx.xy), everything after the period, is output, you keep the output, but substitute the variable (named before the period) with the provided input. A lambda expression is like a function, you call the function by substituting the input throughout the expression. This is the process of calling the lambda expression with input, and getting the output. The result is equivalent to what you start out with, just with different variable names.Ģ) Beta Reduction - Basically just substitution. For example (λx.xx)(λx.x) becomes something like (λx.xx)(λy.y) or (λx.xx)(λx'.x') after reduction. There are basically two and a half processes in lambda calculus:ġ) Alpha Conversion - if you are applying two lambda expressions with the same variable name inside, you change one of them to a new variable name. Lambdas are like a function or a method - if you are familiar with programming, they are functions that take a function as input, and return a new function as output. In lambda calculus, there are only lambdas, and all you can do with them is substitution. Starting from $0$, a successor function is needed to yield $1$.Lambda calculus has a way of spiraling into a lot of steps, making solving problems tedious, and it can look real hard, but it isn't actually that bad. a function which maps any real value to its product with itself, is usually notated like this:į: \mathbb$ can be constructed: To give an example: The square function, i.e. It associates values in the input set, the domain of a function, to exactly one value of the output set, the codomain of the function. Since lambda calculus is all about computable functions, a basic understanding of functions and its properties is useful.Ī function, in its mathematical sense, describes the relation between a set of possible input and a set of possible output values. The goal of this article is to introduce some basic concepts of lambda calculus, which later on can be mapped to real world usage scenarios with functional programming languages. Although the topic might seem very theoretical, some basic knowledge in lambda calculus can be very helpful to understand these languages, and where they originated from, much better. Introduced in the 1930s by Alonzo Church, it is (in its typed form) the fundamental concept of functional programming languages like Haskell and Scala. Lambda calculus is a formal system to study computable functions based on variable binding and substitution.



 0 kommentar(er)
0 kommentar(er)
